Derham sequence (3D)#

Bases: object

The discrete Derham sequence on the logical unit cube (3d).

Check out the corresponding Struphy API for a hands-on introduction.

The tensor-product discrete deRham complex is loaded using the Psydac API and then augmented with polar sub-spaces (indicated by a bar) and boundary operators.

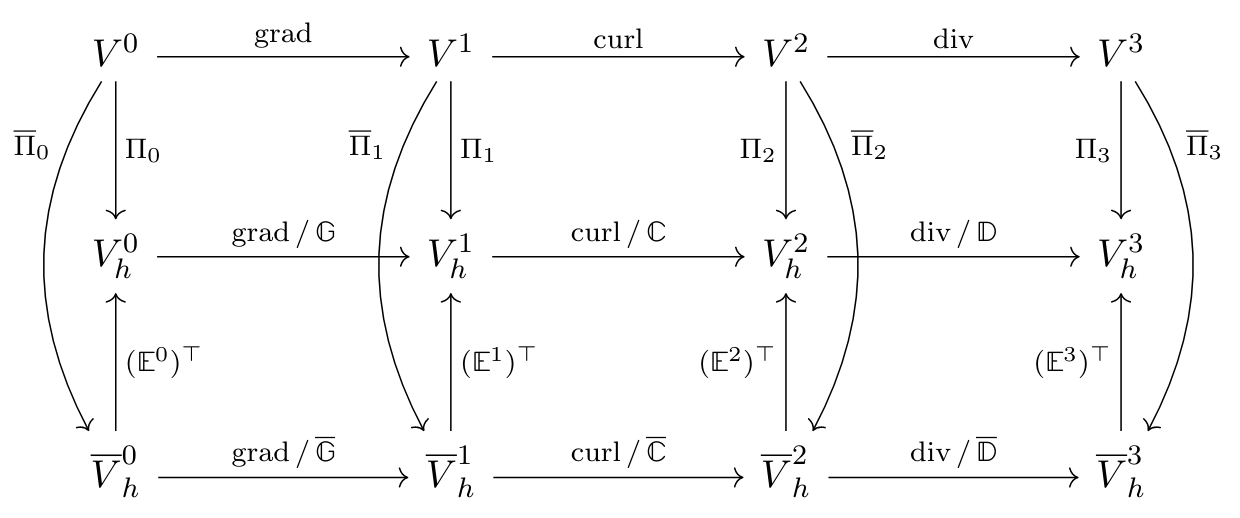
Parameters:

Nel (list[int]) – Number of elements in each direction.
p (list[int]) – Spline degree in each direction.
spl_kind (list[bool]) – Kind of spline in each direction (True=periodic, False=clamped).
dirichlet_bc (list[list[bool]]) – Whether to apply homogeneous Dirichlet boundary conditions (at left or right boundary in each direction).
nq_pr (list[int]) – Number of Gauss-Legendre quadrature points in each direction for geometric projectors (default = p+1, leads to exact integration of degree 2p+1 polynomials).
nquads (list[int]) – Number of Gauss-Legendre quadrature points in each direction (default = p, leads to exact integration of degree 2p-1 polynomials).
comm (mpi4py.MPI.Intracomm) – MPI communicator (within a clone if domain cloning is used, otherwise MPI.COMM_WORLD)
mpi_dims_mask (list of bool) – True if the dimension is to be used in the domain decomposition (=default for each dimension). If mpi_dims_mask[i]=False, the i-th dimension will not be decomposed.
with_projectors (bool) – Whether to add global commuting projectors to the diagram.
polar_ck (int) – Smoothness at a polar singularity at eta_1=0 (default -1 : standard tensor product splines, OR 1 : C1 polar splines)
local_projectors (bool) – Whether to build the local commuting projectors based on quasi-inter-/histopolation.
domain (struphy.geometry.base.Domain) – Mapping from logical unit cube to physical domain (only needed in case of polar splines polar_ck=1).

property Nel#: List of number of elements (=cells) in each direction.

property p#: List of B-spline degrees in each direction.

property spl_kind#: List of spline type (periodic=True or clamped=False) in each direction.

property dirichlet_bc#: None, or list of boundary conditions in each direction. Each entry is a list with two entries (left and right boundary), “d” (hom. Dirichlet) or None (periodic).

property nquads#: List of number of Gauss-Legendre quadrature points in each direction (default = p, leads to exact integration of degree 2p-1 polynomials).

property nq_pr#: List of number of Gauss-Legendre quadrature points in histopolation (default = p + 1) in each direction.

property with_local_projectors#: True if local projectors are to be used instead of the default global ones.

property comm#: MPI communicator.

property polar_ck#: C^k smoothness at eta_1=0.

property breaks#: List of break points (=cell interfaces) in each direction.

property indN#: List of 2d arrays holding global spline indices (N) in each element in the three directions.

property indD#: List of 2d arrays holding global spline indices (D) in each element in the three directions.

property domain_decomposition#: Psydac’s domain decomposition object (same for all vector spaces!).

property domain_array#

A 2d array[float] of shape (comm.Get_size(), 9). The row index denotes the process number and for n=0,1,2:

domain_array[i, 3*n + 0] holds the LEFT domain boundary of process i in direction eta_(n+1).

domain_array[i, 3*n + 1] holds the RIGHT domain boundary of process i in direction eta_(n+1).

domain_array[i, 3*n + 2] holds the number of cells of process i in direction eta_(n+1).

property breaks_loc#: The domain local to this process.

property index_array#

A 2d array[int] of shape (comm.Get_size(), 6). The row index denotes the process number and for n=0,1,2:

arr[i, 2*n + 0] holds the global start index of cells of process i in direction eta_(n+1).

arr[i, 2*n + 1] holds the global end index of cells of process i in direction eta_(n+1).

property index_array_N#

A 2d array[int] of shape (comm.Get_size(), 6). The row index denotes the process number and for n=0,1,2:

arr[i, 2*n + 0] holds the global start index of B-splines (N) of process i in direction eta_(n+1).

arr[i, 2*n + 1] holds the global end index of B-splines (N) of process i in direction eta_(n+1).

property index_array_D#

A 2d array[int] of shape (comm.Get_size(), 6). The row index denotes the process number and for n=0,1,2:

arr[i, 2*n + 0] holds the global start index of M-splines (D) of process i in direction eta_(n+1).

arr[i, 2*n + 1] holds the global end index of M-splines (D) of process i in direction eta_(n+1).

property neighbours#: A 3d array[int] with shape (3,3,3). It contains the 26 neighbouring process ids (rank). This is done in terms of N-spline start/end indices. The i-th index indicates direction eta_(i+1). 0 is a left neighbour, 1 is the same plane as the current process, 2 is a right neighbour. For more detail see _get_neighbours().

property space_to_form#: Dictionary containing the names of the continuous spaces and corresponding discrete spaces.

property Vh#: Dictionary containing finite-dimensional vector spaces (sub-spaces of continuous spaces, Stencil-/BlockVectorSpace).

property Vh_fem#: Dictionary containing FEM spline spaces (TensorFem-/VectorFemSpace).

property nbasis#: Dictionary containing number of 1d basis functions for each component and spatial direction.

property spline_types#: Dictionary holding 1d spline types for each component and spatial direction, entries either ‘B’ or ‘M’.

property spline_types_pyccel#: Dictionary holding 1d spline types for each component and spatial direction, entries either 0 (=’B’) or 1 (=’M’).

property proj_grid_pts#: Dictionary of quadrature points for histopolation (or Greville points for interpolation) in format (ii, iq) = (interval, quadrature point).

property proj_grid_wts#: Dictionary of quadrature weights for histopolation (or 1’s for interpolation) in format (ii, iq) = (interval, quadrature point).

property proj_grid_subs#: Dictionary of histopolation subintervals (or 0’s for interpolation) as 1d arrays. A value of 1 indicates that the corresponding cell is the second subinterval of a split Greville cell (for histopolation with even degree).

property quad_grid_pts#: Dictionary of quadrature points for integration over grid cells in format (ni, nq) = (cell, quadrature point).

property quad_grid_wts#: Dictionary of quadrature weights for integration over grid cells in format (ni, nq) = (cell, quadrature point).

property quad_grid_spans#: Dictionary of knot span indices of grid cells.

property quad_grid_bases#: Dictionary of basis functions evaluated at quadrature grids in format (ni, bl, 0, nq) = (cell, basis function, derivative=0, quadrature point).

property extraction_ops#: Dictionary holding basis extraction operators, either IdentityOperator or PolarExtractionOperator.

property dofs_extraction_ops#: Dictionary holding dof extraction operators for commuting projectors, either IdentityOperator or PolarExtractionOperator.

property boundary_ops#: Dictionary holding essential boundary operators (BoundaryOperator) OR IdentityOperators.

property P#: Dictionary holding global commuting projectors.

property Vh_pol#: Polar sub-spaces, either PolarDerhamSpace (with polar splines) or Stencil-/BlockVectorSpace (same as self.Vh)

property grad_bcfree#: Discrete gradient Vh0_pol (H1) -> Vh1_pol (Hcurl) w/o boundary operator.

property curl_bcfree#: Discrete curl Vh1_pol (Hcurl) -> Vh2_pol (Hdiv) w/o boundary operator.

property div_bcfree#: Discrete divergence Vh2_pol (Hdiv) -> Vh3_pol (L2) w/o boundary operator.

property grad#: Discrete gradient Vh0_pol (H1) -> Vh1_pol (Hcurl).

property curl#: Discrete curl Vh1_pol (Hcurl) -> Vh2_pol (Hdiv).

property div#: Discrete divergence Vh2_pol (Hdiv) -> Vh3_pol (L2).

property args_derham#: Collection of mandatory arguments for pusher kernels.

Discretize the Derahm complex. Allows for the use of tiny-psydac.

Parameters:

Nel (list[int]) – Number of elements in each direction.
p (list[int]) – Spline degree in each direction.
spl_kind (list[bool]) – Kind of spline in each direction (True=periodic, False=clamped).
comm (mpi4py.MPI.Intracomm) – MPI communicator (within a clone if domain cloning is used, otherwise MPI.COMM_WORLD)
mpi_dims_mask (list of bool) – True if the dimension is to be used in the domain decomposition (=default for each dimension). If mpi_dims_mask[i]=False, the i-th dimension will not be decomposed.

Creat a callable spline function.

Parameters:

name (str) – Field’s key to be used for instance when saving to hdf5 file.
space_id (str) – Space identifier for the field (“H1”, “Hcurl”, “Hdiv”, “L2” or “H1vec”).
coeffs (StencilVector | BlockVector) – The spline coefficients.
backgrounds (FieldsBackground | list) – For the initial condition.
perturbations (Perturbation | list) – For the initial condition.
domain (Domain) – Mapping for pullback/transform of initial condition.
equil (FLuidEquilibrium) – Fluid background used for inital condition.

prepare_eval_tp_fixed(grids_1d)[source]#

Obtain knot span indices and spline basis functions evaluated at tensor product grid.

Parameters:

grids_1d (3-list of 1d arrays) – Points of the tensor product grid.

Returns:

spans (3-tuple of 2d int arrays) – Knot span indices in each direction in format (n, nq).
bns (3-tuple of 3d float arrays) – Values of p + 1 non-zero B-Splines at quadrature points in format (n, nq, basis).
bds (3-tuple of 3d float arrays) – Values of p non-zero D-Splines at quadrature points in format (n, nq, basis).

get_quad_grids(space: TensorFemSpace | VectorFemSpace, nquads: list | tuple | None = None)[source]#: Return the 1d quadrature grids in each direction as a tuple.

Bases: object

Initializes a callable spline function with a method for assigning initial conditions.

Parameters:

name (str) – Field’s key to be used for instance when saving to hdf5 file.
space_id (str) – Space identifier for the field (“H1”, “Hcurl”, “Hdiv”, “L2” or “H1vec”).
derham (struphy.feec.psydac_derham.Derham) – Discrete Derham complex.
coeffs (StencilVector | BlockVector) – The spline coefficients (optional).
backgrounds (FieldsBackground | list) – For the initial condition.
perturbations (Perturbation | list) – For the initial condition.
domain (Domain) – Mapping for pullback/transform of initial condition.
equil (FluidEquilibrium) – Fluid background used for inital condition.

property name#: Name of the field in data container (string).

property space_id#

‘H1’, ‘Hcurl’, ‘Hdiv’, ‘L2’ or ‘H1vec’.

Type:: String identifying the continuous space of the field

property space_key#

‘0’, ‘1’, ‘2’, ‘3’ or ‘v’.

Type:: String identifying the discrete space of the field

property derham#: 3d Derham complex struphy.feec.psydac_derham.Derham.

property domain#: Mapping for pullback/transform of initial condition.

property equil#: Fluid equilibirum used for initial condition.

property space#: Coefficient space (VectorSpace) of the field.

property fem_space#: FE space (FemSpace) of the field.

property ET#: Transposed PolarExtractionOperator (or IdentityOperator) for mapping polar coeffs to polar tensor product rings.

property vector#: psydac.linalg.stencil.StencilVector or psydac.linalg.block.BlockVector or struphy.polar.basic.PolarVector.

property starts#: Global indices of the first FE coefficient on the process, in each direction.

property ends#: Global indices of the last FE coefficient on the process, in each direction.

property pads#: Paddings for ghost regions, in each direction.

property nbasis#: Tuple(s) of 1d dimensions for each direction.

property vector_stencil#

Tensor-product Stencil-/BlockVector corresponding to a copy of self.vector in case of Stencil-/Blockvector

OR

the extracted coefficients in case of PolarVector. Call self.extract_coeffs() beforehand.

property backgrounds: FieldsBackground | list#: For the initial condition.

property perturbations: Perturbation | list#: For the initial condition.

extract_coeffs(update_ghost_regions=True)[source]#

Maps polar coeffs to polar tensor product rings in case of PolarVector (written in-place to self.vector_stencil) and updates ghost regions.

Parameters:: update_ghost_regions (bool) – If the ghost regions shall be updated (needed in case of non-local acccess, e.g. in field evaluation).

initialize_coeffs(*, backgrounds: FieldsBackground | list | None = None, perturbations: Perturbation | list | None = None, domain: Domain | None = None, equil: FluidEquilibrium | None = None)[source]#: Set the initial conditions for self.vector.

initialize_coeffs_from_restart_file(file, species=None)[source]#: TODO

eval_tp_fixed_loc(spans, bases, out=None)[source]#

Spline evaluation on pre-defined grid.

Input spans must be on local process, start <= span <= end.

Parameters:

spans (3-tuple of 1d int arrays) – Knot span indices in each direction (start <= span <= end).
bases (3-tuple of 2d float arrays) – Values of non-zero eta basis functions at evaluation points indexed by (eta, basis function).

Returns:

out – 3d array of spline values S_ijk corresponding to the sizes of spans.

Return type:

array[float]

class struphy.feec.psydac_derham.DiscreteDerham(*spaces)[source]#

Bases: object

A discrete de Rham sequence in 3D.

Parameters:: *spaces (list of TensorFemSpace | VectorFemSpace) – The discrete spaces of the de Rham sequence.

property dim#: Dimension of the physical and logical domains, which are assumed to be the same.

property V0#

H1 space

Type:: First space of the de Rham sequence

property V1#: Second space of the de Rham sequence: - 1d : L2 space - 2d : either Hdiv or Hcurl space - 3d : Hcurl space

property V2#: Third space of the de Rham sequence: - 2d : L2 space - 3d : Hdiv space

property V3#

L2 space in 3d

Type:: Fourth space of the de Rham sequence

property spaces#: Spaces of the proper de Rham sequence (excluding Hvec).

property derivatives_as_matrices#: Differential operators of the De Rham sequence as LinearOperator objects.

property derivatives#

Differential operators of the De Rham sequence as DiffOperator objects.

Those are objects with domain and codomain properties that are FemSpace, they act on FemField (they take a FemField of their domain as input and return a FemField of their codomain.

projectors(*, kind='global', nquads=None)[source]#

Projectors mapping callable functions of the physical coordinates to a corresponding FemField object in the De Rham sequence.

Parameters:

kind (str) – Type of the projection : at the moment, only global is accepted and returns geometric commuting projectors based on interpolation/histopolation for the De Rham sequence (GlobalProjector objects).
nquads (list(int) | tuple(int)) – Number of quadrature points along each direction, to be used in Gauss quadrature rule for computing the (approximated) degrees of freedom.

Returns:

P0, …, Pn – Projectors that can be called on any callable function that maps from the physical space to R (scalar case) or R^d (vector case) and returns a FemField belonging to the i-th space of the De Rham sequence

Return type:

callables

struphy.feec.psydac_derham.transform_perturbation(pert_type: str, pert_params: dict, space_key: str, domain: Domain)[source]#

Creates callabe(s) from perturbation parameters.

Parameters:

pert_type (str) – Class name of the perturbation, see perturbations.
pert_params (dict) – Parameters of the perturbation.
space_key (str) – The p-form representation of the output: ‘0’, ‘1’, ‘2’ ‘3’ or ‘v’.
domain (Domain) – Domain object (mapping).

Returns:

fun – A callable or list of callables in the space defined by space_key.

Return type:

list

struphy.feec.psydac_derham.get_pts_and_wts(space_1d, start, end, n_quad=None, polar_shift=False)[source]#

Obtain local (to MPI process) projection point sets and weights in one grid direction.

Parameters:

space_1d (SplineSpace) – Psydac object for uni-variate spline space.
start (int) – Start index on current process.
end (int) – End index on current process.
n_quad (int) – Number of quadrature points for Gauss-Legendre histopolation. If None, is set to p + 1 where p is the space_1d degree (products of basis functions are integrated exactly).
polar_shift (bool) – Whether to shift the first interpolation point away from 0.0 by 1e-5 (needed only in eta_1 and for polar domains).

Returns:

pts (2D float array) – Quadrature points (or Greville points for interpolation) in format (ii, iq) = (interval, quadrature point).
wts (2D float array) – Quadrature weights (or 1’s for interpolation) in format (ii, iq) = (interval, quadrature point).
subs (1D int array) – One entry for each interval ii; usually has value 0. A value of 1 indicates that the cell ii is the second subinterval of a split Greville cell (for histopolation with even degree).

struphy.feec.psydac_derham.get_pts_and_wts_quasi(space_1d: SplineSpace, *, bulk_indices_i: tuple | None = None, mu_nu_values: list | None = None, polar_shift: bool = False)[source]#

Obtain local projection point sets and weights in one grid direction for the quasi-interpolation method. The quasi-interpolation points are $\nu - \mu +p$ equidistant points $\{ x^i_j \}_{0 \leq j < \nu - \mu +p}$ in the sub-interval $Q = [\eta_\mu , \eta_\nu]$ given by:

begin{itemize}

item Clamped: .. math:

Q = \left\{\begin{array}{lr}
[\eta_p = 0, \eta_{p+1}], & i = 0 \,,\\
{[\eta_p = 0, \eta_{p+i}]}, & 0 < i < p-1\,,\\
{[\eta_{i+1}, \eta_{i+p}]}, & p-1 \leq i \leq \hat{n}_N - p\,,\\
{[\eta_{i+1}, \eta_{\hat{n}_N} = 1]}, &  \hat{n}_N - p < i < \hat{n}_N -1\,,\\
{[\eta_{\hat{n}_N -1}, \eta_{\hat{n}_N} = 1]}, & i = \hat{n}_N -1 \,.
\end{array} \; \right .

item Periodic: .. math:

Q = [\eta_{i + 1}, \eta_{i + p}] \:\:\:\:\: \forall \:\: i.

end{itemize}

Which are allways a subset of $\{-(p-1)h,-(p-1)h + \frac{h}{2}, ..., 1-h - \frac{h}{2},1-h \}$ for the periodic case.

Parameters:

space_1d (SplineSpace) – Psydac object for uni-variate spline space.
polar_shift (bool) – Whether to shift the first interpolation point away from 0.0 by 1e-5 (needed only in eta_1 and for polar domains).

Returns:

pts (2D float array) – Quadrature points (or quasi-interpolation points for interpolation) in format (ii, iq) = (interval, quadrature point).
wts (2D float array) – Quadrature weights (or 1’s for interpolation) in format (ii, iq) = (interval, quadrature point).

struphy.feec.psydac_derham.get_span_and_basis(pts, space)[source]#

Compute the knot span index and the values of p + 1 basis function at each point in pts.

Parameters:

pts (xp.array) – 2d array of points (ii, iq) = (interval, quadrature point).
space (SplineSpace) – Psydac object, the 1d spline space to be projected.

Returns:

span (xp.array) – 2d array indexed by (n, nq), where n is the interval and nq is the quadrature point in the interval.
basis (xp.array) – 3d array of values of basis functions indexed by (n, nq, basis function).

struphy.feec.psydac_derham.get_weights_local_projector(pts, fem_space)[source]#

Compute the geometric weights for interpolation and histopolation. Should be called only with the grid points for 0-forms.

Parameters:

pts (xp.array) – 3d array of points. Contains the quasi-interpolation points in each direction.
fem_space (SplineSpace) – Psydac object, the 1d spline space to be projected. Should be the 0-form space.

Returns:

wij (List of xp.array) – List of 2d array indexed by (space_direction, i, j), where i determines for which FEEC coefficient this weights are needed. Used for interpolation.
whij (List of xp.array) – List of 2d array indexed by (space_direction, i, j), where i determines for which FEEC coefficient this weights are needed. Used for histopolation.

struphy.feec.psydac_derham.select_basis_local(i, p, Nbasis, periodic)[source]#

Determines the start and end indices of the basis functions that must be taken from the collocation matrix to compute the geometric weights wij, for any given i.

Parameters:

i (int) – Index of the wij weights that must be computed.
p (int) – B-spline degree.
Nbasis (int) – Number of B-spline.
periodic (bool) – Whether we have periodic boundary conditions.

Returns:

start (int) – Start index of the B-splines that must be consider in the collocation matrix to obtain the wij weights. Inclusive index
end (int) – End index of the B-splines that must be consider in the collocation matrix to obtain the wij weights. Exclusive index

class psydac.fem.tensor.TensorFemSpace(domain_decomposition, *spaces, coeff_space=None, cart=None, dtype=<class 'float'>)[source]#

Bases: FemSpace

Tensor-product Finite Element space V.

Parameters:

domain_decomposition (psydac.ddm.cart.DomainDecomposition)
*spaces (psydac.fem.splines.SplineSpace) – 1D finite element spaces.
coeff_space (psydac.linalg.stencil.StencilVectorSpace or None) – The vector space to which the coefficients belong (optional).
cart (psydac.ddm.CartDecomposition or None) – Object that contains all information about the Cartesian decomposition of a tensor-product grid of coefficients.
dtype ({float, complex}) – Data type of the coefficients.

Notes

For now we assume that this tensor-product space can ONLY be constructed from 1D spline spaces.

property ldim#: Parametric dimension.

property periodic#

along each logical dimension, say if domain is periodic. :rtype: tuple[bool]

Type:: Tuple of booleans

property domain_decomposition#

property mapping#: Mapping from logical coordinates ‘eta’ to physical coordinates ‘x’. If None, we assume identity mapping (hence x=eta).

property coeff_space#: Vector space of the coefficients (mapping invariant). :rtype: psydac.linalg.stencil.StencilVectorSpace

property interfaces#

property symbolic_space#: Symbolic space.

property patch_spaces#: Return the patch spaces (self if single-patch) as a tuple.

property component_spaces#: Return the component spaces (self if scalar-valued) as a tuple.

property axis_spaces#: Return the axis spaces (self if univariate) as a tuple.

property is_multipatch#: Boolean flag that describes whether the space is a multi-patch space. :rtype: bool

property is_vector_valued#: Boolean flag that describes whether the space is vector-valued. :rtype: bool

eval_field(field, *eta, weights=None)[source]#

Evaluate field at location(s) eta.

Parameters:

field (FemField) – Field object (element of FemSpace) to be evaluated.
eta (list of float or numpy.ndarray) – Evaluation point(s) in logical domain.
weights (StencilVector, optional) – Weights of the basis functions, such that weights.space == field.coeffs.space.

Returns:

value – Field value(s) at location(s) eta.

Return type:

float or numpy.ndarray

preprocess_regular_tensor_grid(grid, der=0, overlap=0)[source]#

Returns all the quantities needed to evaluate fields on a regular tensor-grid.

Parameters:

grid (List of ndarray) – List of 2D arrays representing each direction of the grid. Each of these arrays should have shape (ne_xi, nv_xi) where ne_xi is the number of cells in the domain in the direction xi and nv_xi is the number of evaluation points in the same direction.
der (int, default=0) – Number of derivatives of the basis functions to pre-compute.
overlap (int) – How much to overlap. Only used in the distributed context.

Returns:

degree (tuple of int) – Degree in each direction
global_basis (List of ndarray) – List of 4D arrays, one per direction, containing the values of the p+1 non-vanishing basis functions (and their derivatives) at each grid point. The array for direction xi has shape (ne_xi, der + 1, p+1, nv_xi).
global_spans (List of ndarray) – List of 1D arrays, one per direction, containing the index of the last non-vanishing basis function in each cell. The array for direction xi has shape (ne_xi,).
local_shape (List of tuple) – Shape of what is local to this instance.

preprocess_irregular_tensor_grid(grid, der=0, overlap=0)[source]#

Returns all the quantities needed to evaluate fields on a regular tensor-grid.

Parameters:

grid (List of ndarray) – List of 1D arrays representing each direction of the grid.
der (int, default=0) – Number of derivatives of the basis functions to pre-compute.
overlap (int) – How much to overlap. Only used in the distributed context.

Returns:

pads (tuple of int) – Padding in each direction
degree (tuple of int) – Degree in each direction
global_basis (List of ndarray) – List of 4D arrays, one per direction, containing the values of the p+1 non-vanishing basis functions (and their derivatives) at each grid point. The array for direction xi has shape (n_xi, p+1, der + 1).
global_spans (List of ndarray) – List of 1D arrays, one per direction, containing the index of the last non-vanishing basis function in each cell. The array for direction xi has shape (n_xi,).
cell_indexes (list of ndarray) – List of 1D arrays, one per direction, containing the index of the cell in which the corresponding point in grid is.
local_shape (List of tuple) – Shape of what is local to this instance.

eval_fields(grid, *fields, weights=None, npts_per_cell=None, overlap=0)[source]#

Evaluate one or several fields at the given location(s) grid.

Parameters:

grid (List of ndarray) – Grid on which to evaluate the fields
*fields (tuple of psydac.fem.basic.FemField) – Fields to evaluate
weights (psydac.fem.basic.FemField or None, optional) – Weights field.
npts_per_cell (int or tuple of int or None, optional) – number of evaluation points in each cell. If an integer is given, then assume that it is the same in every direction.
overlap (int) – How much to overlap. Only used in the distributed context.

Returns:

List of the evaluated fields.

Return type:

List of ndarray of floats

eval_fields_regular_tensor_grid(grid, *fields, weights=None, overlap=0)[source]#

Evaluate fields on a regular tensor grid

Parameters:

grid (List of ndarray) – List of 2D arrays representing each direction of the grid. Each of these arrays should have shape (ne_xi, nv_xi) where ne is the number of cells in the domain in the direction xi and nv_xi is the number of evaluation points in the same direction.
*fields (tuple of psydac.fem.basic.FemField) – Fields to evaluate on grid.
weights (psydac.fem.basic.FemField or None, optional) – Weights to apply to our fields.
overlap (int) – How much to overlap. Only used in the distributed context.

Returns:

Values of the fields on the regular tensor grid

Return type:

List of ndarray of float

eval_fields_irregular_tensor_grid(grid, *fields, weights=None, overlap=0)[source]#

Evaluate fields on a regular tensor grid

Parameters:

grid (List of ndarray) – List of 2D arrays representing each direction of the grid. Each of these arrays should have shape (ne_xi, nv_xi) where ne is the number of cells in the domain in the direction xi and nv_xi is the number of evaluation points in the same direction.
*fields (tuple of psydac.fem.basic.FemField) – Fields to evaluate on grid.
weights (psydac.fem.basic.FemField or None, optional) – Weights to apply to our fields.
overlap (int) – How much to overlap. Only used in the distributed context.

Returns:

Values of the fields on the regular tensor grid

Return type:

List of ndarray of float

eval_field_gradient(field, *eta, weights=None)[source]#

Evaluate field gradient at location(s) eta.

Parameters:

field (FemField) – Field object (element of FemSpace) to be evaluated.
eta (list of float or numpy.ndarray) – Evaluation point(s) in logical domain.
weights (StencilVector, optional) – Weights of the basis functions, such that weights.space == field.coeffs.space.

Returns:

value – Value(s) of field gradient at location(s) eta.

Return type:

float or numpy.ndarray

integral(f, *, nquads=None)[source]#

property dtype#

property nbasis#

property knots#

property breaks#

property degree#

property multiplicity#

property pads#

property ncells#

property spaces#

get_assembly_grids(*nquads)[source]#

Return a tuple of FemAssemblyGrid objects (one for each direction).

These objects are local to the process, and contain all 1D information which is necessary for the correct assembly of the l.h.s. matrix and r.h.s. vector in a finite element method. This information includes the coordinates and weights of all quadrature points, as well as the values of the non-zero basis functions, and their derivatives, at such points.

The computed FemAssemblyGrid objects are stored in a dictionary in self with nquads as key, and are reused if a match is found.

Parameters:: *nquads (int) – Number of quadrature points per cell, along each direction.
Returns:: The 1D assembly grids along each direction.
Return type:: tuple of FemAssemblyGrid

property local_domain#

Logical domain local to the process, assuming the global domain is decomposed across processes without any overlapping.

This information is fundamental for avoiding double-counting when computing integrals over the global domain.

Returns:

element_starts (tuple of int) – Start element index along each direction.
element_ends (tuple of int) – End element index along each direction.

property global_element_starts#

property global_element_ends#

property eta_lims#

Eta limits of domain local to the process (for field evaluation).

Returns:: eta_limits – Along each dimension i, limits are given as (eta^i_{min}, eta^i_{max}).
Return type:: tuple of (2-tuple of float)

init_interpolation()[source]#

init_histopolation()[source]#

compute_interpolant(values, field)[source]#

Compute field (i.e. update its spline coefficients) such that it interpolates a certain function $f(x1,x2,..)$ at the Greville points.

Parameters:

values (StencilVector) – Function values $f(x_i)$ at the n-dimensional tensor grid of Greville points $x_i$, to be interpolated.
field (FemField) – Input/output argument: tensor spline that has to interpolate the given values.

reduce_grid(axes=(), knots=())[source]#

Create a new TensorFemSpace object with a coarser grid than the original one we do that by giving a new knot sequence in the desired dimension.

Parameters:

axes (List of int) – Dimensions where we want to coarsen the grid.
knots (List or tuple) – New knot sequences in each dimension.

Returns:

V – New space with a coarser grid.

Return type:

TensorFemSpace

export_fields(filename, **fields)[source]#: Write spline coefficients of given fields to HDF5 file.

import_fields(filename, *field_names)[source]#

Load fields from HDF5 file containing spline coefficients.

Parameters:

filename (str) – Name of HDF5 input file.
field_names (list of str) – Names of the datasets with the required spline coefficients.

Returns:

fields – Distributed fields, given in the same order of the names.

Return type:

list of FemSpace objects

reduce_degree(axes, multiplicity=None, basis='B')[source]#

add_refined_space(ncells)[source]#: refine the space with new ncells and add it to the dictionary of refined_space

create_interface_space(axis, ext, cart)[source]#

Create a new interface fem space along a given axis and extremity.

Parameters:

axis (int) – The axis of the new Interface space.
ext (int) – The extremity of the new Interface space. the values must be 1 or -1.
cart (CartDecomposition) – The cart of the new space, needed in the parallel case.

get_refined_space(ncells)[source]#

set_refined_space(ncells, new_space)[source]#

plot_2d_decomposition(mapping=None, refine=10)[source]#

class psydac.fem.vector.VectorFemSpace(*spaces)[source]#

Bases: FemSpace

FEM space with a vector basis defined on a single patch. This class is used to represent either spaces of vector-valued FEM fields, or product spaces involved in systems of equations.

Parameters:: *spaces (FemSpace) – Single-patch FEM spaces, either scalar or vector-valued.

property ldim#: Parametric dimension.

property periodic#

along each logical dimension, say if domain is periodic. :rtype: tuple[bool]

Type:: Tuple of booleans

property mapping#: Mapping from logical coordinates ‘eta’ to physical coordinates ‘x’. If None, we assume identity mapping (hence x=eta).

property coeff_space#: Vector space of the coefficients (mapping invariant). :rtype: psydac.linalg.block.BlockVectorSpace

property symbolic_space#: Symbolic space.

property patch_spaces#: Return the patch spaces (self if single-patch) as a tuple.

property component_spaces#: Return the component spaces (self if scalar-valued) as a tuple.

property axis_spaces#: Return the axis spaces (self if univariate) as a tuple.

property is_multipatch#: Boolean flag that describes whether the space is a multi-patch space. :rtype: bool

property is_vector_valued#: Boolean flag that describes whether the space is vector-valued. :rtype: bool

eval_field(field, *eta, weights=None)[source]#

Evaluate field at location(s) eta.

Parameters:

field (FemField) – Field object (element of FemSpace) to be evaluated.
eta (list of float or numpy.ndarray) – Evaluation point(s) in logical domain.
weights (StencilVector, optional) – Weights of the basis functions, such that weights.space == field.coeffs.space.

Returns:

value – Field value(s) at location(s) eta.

Return type:

float or numpy.ndarray

eval_fields(grid, *fields, weights=None, npts_per_cell=None, overlap=0)[source]#

Evaluates one or several fields on the given location(s) grid.

Parameters:

grid (List of ndarray) – Grid on which to evaluate the fields. Each array in this list corresponds to one logical coordinate.
*fields (tuple of psydac.fem.basic.FemField) – Fields to evaluate.
weights (psydac.fem.basic.FemField or None, optional) – Weights field used to weight the basis functions thus turning them into NURBS. The same weights field is used for all of fields and they thus have to use the same basis functions.
npts_per_cell (int, tuple of int or None, optional) – Number of evaluation points in each cell. If an integer is given, then assume that it is the same in every direction.
overlap (int) – How much to overlap. Only used in the distributed context.

Returns:

List of the same length as fields, containing for each field a list of self.ldim arrays, i.e. one array for each logical coordinate.

Return type:

List of list of ndarray

Table of Contents

Derham sequence (3D)#

This Page